Sift : Descriptor

07 September 2013

特征描述子

确定描述子采样区域

SIFT 描述子 $h(x, y, \theta)$ 是对特征点附近邻域内高斯图像梯度统计结果的一种表示，它是一个三维的阵列，但通常将它表示成一个矢量。矢量是通过对三维阵列按一定规律进行排列得到的。特征描述子与特征点所在的尺度有关，因此，对梯度的求取应在特征点对应的高斯图像上进行。将特征点附近邻域划分成 $B_p \times B_p$ 个子区域，每个子区域的尺寸为 $m\sigma$ 个像元，其中，$m=3$，$B_p=4$。$\sigma$ 为特征点的尺度值。考虑到实际计算时，需要采用双线性插值，计算的图像区域为 $m\sigma(B_p+1)$。如果再考虑旋转的因素，那么，实际计算的图像区域应大 $m\sigma(B_p+ 1)\sqrt{2}$。

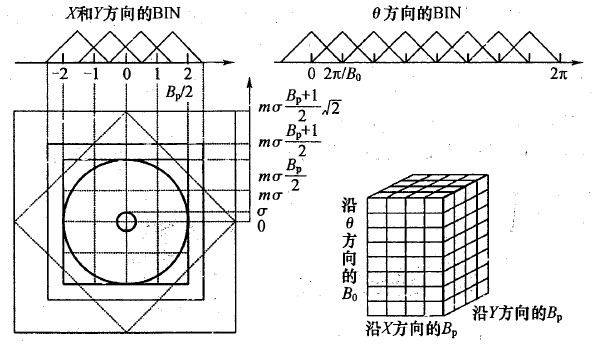
Drawing

生成描述子

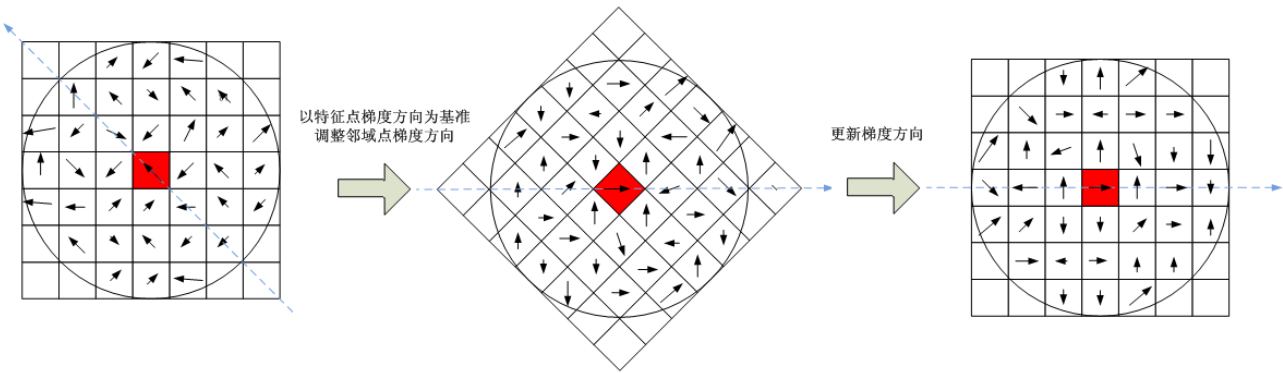
旋转图像至主方向

为了保证特征矢量具有旋转不变性，需要以特征点为中心，将特征点附近邻域内 $(m\sigma(B_p+1)\sqrt{2} \times m\sigma(B_p+1)\sqrt{2})$ 图像梯度的位置和方向旋转一个方向角 $\theta$，即将原图像 x 轴转到与主方向相同的方向。旋转公式如下。

$$ \begin{bmatrix} x'\\ y'\end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} $$

在特征点附近邻域图像梯度的位置和方向旋转后，再以特征点为中心，在旋转后的图像中取一个 $m\sigma B_p \times m\sigma B_p$ 大小的图像区域。并将它等间隔划分成 $B_p \times B_p$ 个子区域，每个间隔为 $m\sigma$像元。

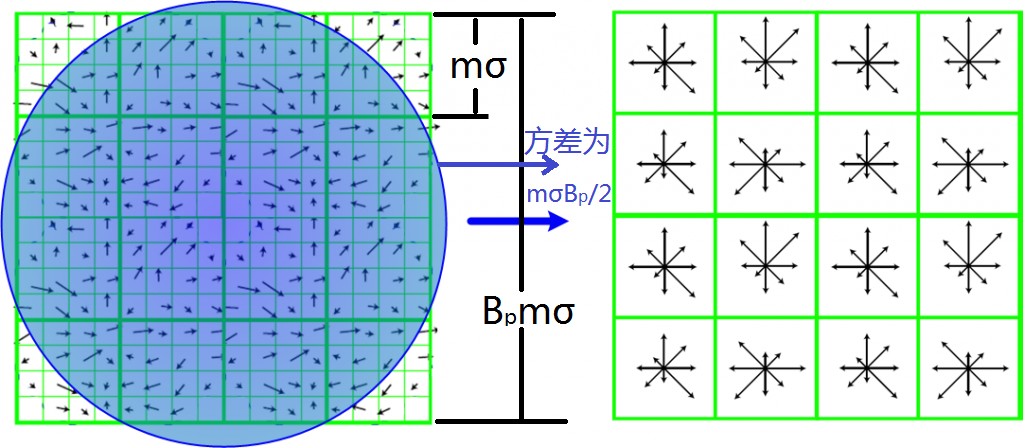
Drawing

生成特征向量

在每子区域内计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，形成一个种子点。与求特征点主方向时有所不同，此时，每个子区域的梯度方向直方图将 0° ~360° 划分为 8 个方向范围，每个范围为 45°，这样，每个种子点共有 8 个方向的梯度强度信息。由于存在 4X4（$B_p \times B_p$）个子区域，所以，共有 4X4X8=128 个数据，最终形成 128 维的 SIFT 特征矢量。同样，对于特征矢量需要进行高斯加权处理，加权采用方差为 $m\sigma B_p/2$ 的标准高斯函数，其中距离为各点相对于特征点的距离。使用高斯权重的是为了防止位置微小的变化给特征向量带来很大的改变，并且给远离特征点的点赋予较小的权重，以防止错误的匹配。

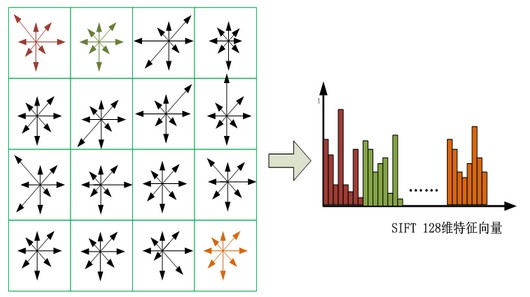
Drawing Drawing

问题1：对于旋转之后的点进行三线性插值，具体是怎样操作的？

Lowe原文如下：

It is important to avoid all boundary affects in which the descriptor abruptly changes as a sample shifts smoothly from being within one histogram to another or from one orientation to another. Therefore, trilinear interpolation is used to distribute the value of each gradient sample into adjacent histogram bins. In other words, each entry into a bin is multiplied by a weight of 1 − d for each dimension, where d is the distance of the sample from the central value of the bin as measured in units of the histogram bin spacing.

表示没看懂 OpenCV 和 vlfeat 中插值这一部分具体实现。

归一化特征向量

为了去除光照变化的影响，需对上述生成的特征向量进行归一化处理，在归一化处理后，对特征矢量大于 0.2 的要进行截断处理，即大于 0.2 的值只取 0.2，然后重新进行一次归一化处理，其目的是为了提高鉴别性。

float nrm2 = 0;
len = d*d*n;
for( k = 0; k < len; k++ )
    nrm2 += dst[k]*dst[k];
float thr = std::sqrt(nrm2)*SIFT_DESCR_MAG_THR; // SIFT_DESCR_MAG_THR = 4
for( i = 0, nrm2 = 0; i < k; i++ )
{
    float val = std::min(dst[i], thr);  //截断大于0.2的值
    dst[i] = val;
    nrm2 += val*val;
}
nrm2 = SIFT_INT_DESCR_FCTR/std::max(std::sqrt(nrm2), FLT_EPSILON); // SIFT_INT_DESCR_FCTR = 512.f

SIFT开源代码：

vlfeat开源图像处理库，其中http://www.vlfeat.org/api/sift.html关于其代码中一些细节和SIFT原理的解释。
RobHess sift
David Lowe Research Projects中的SIFT
OpenCV SIFT

参考资料：

David G. Lowe Distinctive Image Features from Scale-Invariant Keypoints
王永明王贵锦《图像局部不变性特征与描述》

image processing 4

Sift : Descriptor SIFT: 特征描述子