Kd Tree kd-tree
K-dimensional tree
在个人所接触到的际项目中,经常用到最近邻查找。如三维点云的 registration 问题,用到 ICP 算法时,需要求解点云A中各点到点云B中最近的对应点;再如利用 SfM (Structure from Motion) 进行三维重建时,需要求解每幅图像之间的特征匹配,以形成对应的 track。 这些应用中数据量较大,如果利用线性扫描(Brute Force)来求解最近邻,其速度非常慢。kd-tree 则是利用数据的结构信息来加速搜素的一种数据结构。
kd-tree 通过对数据所在空间的不断二分,来构造一个具有描述样本集的结构信息的数据结构。kd-tree 是每个节点都为k维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间( Half-space )。节点左边的子树代表在超平面左边的点,节点右边的子树代表在超平面右边的点。
划分准则
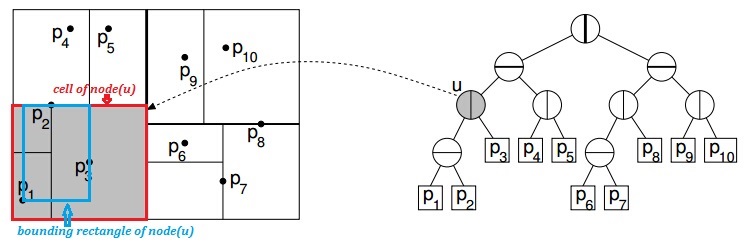
术语
- cell: kd-tree数据结构为把空间递归地划分两个不相交的超矩形(类似于超平面、超立方体的概念),每个超矩形所占的空间即为一个 cell
- bounding rectangle: 包含数据集中所有点的最小超矩形。其范围小于等于该节点对应 cell 的大小
- bucket size: 当相应节点的数据集中点个数大于bucket size,则继续进行子空间划分,否则将不再划分(即成为子叶)。
- aspect ratio: cells 中最长边与最短边的长度比,比值越大,数目 cell 越细长,反之,越肥胖。
- spread: 数据集在某维度上最大值减最小值。即该维度上 bounding rectangle 对应边的长度。
准则
以下介绍 ANN 中提供的几种划分准则:
- standard kd-tree splitting rule:
- 维度(split field)选择: 选择 spread 最大的维度,即 bounding rectangle 中最长边对应的维度。即数据集在该维度上,最大值减最小值的结果为所有维度中最大的维度
- 划分点(pivot)选择: 数据集在该维度上的 中值 (median) [$n\cdot O(\log_{2} n)~or~ O(n^2)$] 作为划分点
- 优点: 划分到左右子树中数据样本相同(或相差1),树的深度为$O(\log_{2} n)$,为平衡二叉树。
- 缺点: 可能出现细长的 cell,易增加回溯时遍历范围。
- midpoint splitting rule:
- 维度(split field)选择: cell 中最长边对应的维度。
- 划分点(pivot)选择: cell 中最长边对应的中心。
- 优点: 找中心比找中值的时间复杂度为低
- 缺点: 导致数据集划分不均匀,当数据高度聚集时,存在很多无用的空间划分(即划分时,所有数据都在一个区域,另一个区域没有数据),树的大小和深度可能会超出$O(n)$。
- sliding midpoint rule: midpoint splitting rule 的改进版 (ANN 推荐使用的划分准则)
- 基本思想: 与 midpoint splitting rule 大致相同,其认为两种划分为好的划分:
- 平衡的划分:使得两个子 cell 都是肥胖的(midpoint splitting rule 中的思想)
- 非平衡的划分:使得较肥胖的 cell 中含有较少的数据点。(对无效划分的处理)
- 划分点选择: 在划分时,当出现无效划分时,通过滑动划分点来消除无效划分,若该维度的中点的值为 a:
- 若所有数据在该维度上都大于 a,则以 数据集中最小值 来划分空间,使用左子树区域中有 1 个点,右子树有 n-1 个点。
- 若所有数据在该维度上都小于 a,则以 数据集中最大值 来划分空间,使用左子树区域中有 n-1 个点,右子树有 1 个点。
- 优点: 通过滑动划分点,可以消除无效的划分,使得树的深度最大为n,空间复杂度为$O(n)$。其可能存在细长的 cell,但其始终伴随着一个该维度上较宽胖的 cell
- 基本思想: 与 midpoint splitting rule 大致相同,其认为两种划分为好的划分:
- fair-split rule:standard kd-tree splitting rule 与 midpoint splitting rule 的折中方案
- 基本思想:设定一个合理的 aspect ratio 值为 a,在划分空间时尽量满足子 cell 的 aspect ratio 小于 a 且尽量使数据均匀的分布在两个子 cell 中。给定一个 cell:
- 根据 cell 各边的长度,选出能够使得划分出两个子 cell 能满足 aspect ratio 小于 a 的所有维度。(midpoint splitting rule 的思想)
- 在上述选出的维度中,选择 bounding rectangle 中最长边对应的维度。
- 在满足 aspect ratio 小于 a 的前提下,在该维度上选择一个使得数据点尽可能分布均匀的划分点来对 cell 进行最终的划分。(standard kd-tree splitting rule 的思想)
- 优点: 相比于 midpoint splitting rule,对于无效的划分,其有更鲁棒的划分结果。然而,当数据高度聚集时,仍有可能出现与 midpoint splitting rule 相同的结果。
- 基本思想:设定一个合理的 aspect ratio 值为 a,在划分空间时尽量满足子 cell 的 aspect ratio 小于 a 且尽量使数据均匀的分布在两个子 cell 中。给定一个 cell:
- sliding fair-split rule:结合 fair-split rule 与 sliding midpoint rule 的思想
- 基本思想: 上述 fair-split rule 划分不能避免:由于必须满足 aspect ratio 小于 a,使得极端情况下,使数据点尽可能的均匀分布的划分 仍然为一个无效划分的情况。此时可以通过滑动划分点至该维上最大(或最小)的值处(即 sliding 的思想)来进行划分(此时无需满足 aspect ratio 小于 a 的条件),使得每个划分都至少含有一个数据点。
无论哪种划分准则,都不会影响 kd-tree 搜索结果的正确性,只会影响其树的形状和深度,从而影响其搜索性能。总的来说,希望得到的 kd-tree 的结构尽量满足两个特点:
- 尽可能的平衡(使搜素深度尽量保持在 $O(\log_{2}{N})$)
- 尽可能的让 cell 肥胖 (使搜索过程中与超矩形体相交的个数尽量少,以减小到达子叶的次数)
构建 kd-tree
术语
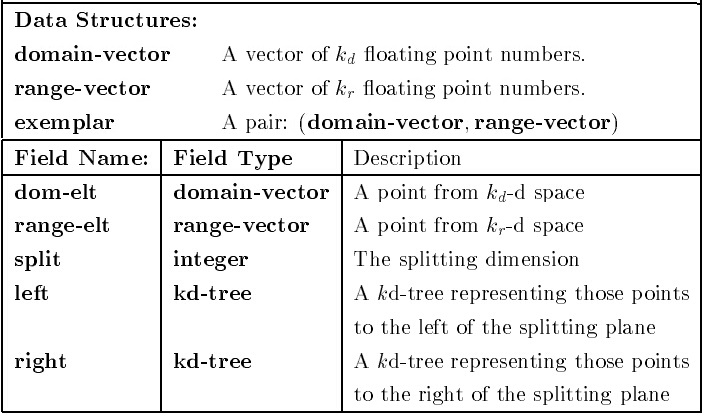
domain-vector: 样本点的值域 range-vector: 样本点范围域(可以暂时忽略) exemplar: 样本点,包含值域和范围域。
算法

$exset\text{-}rep$ : kd-tree 到 样本集 exemplar-set 的一个映射:
$$ exset\text{-}rep:\text{kd-tree} \mapsto \text{exemplar-set} $$ $$ exset\text{-}rep(\text{empty})=\phi $$ $$ exset\text{-}rep(< \textbf{d,r,-},\text{empty,empty}>) = {(\textbf{d,r})} $$ $$ exset\text{-}rep(< \textbf{d,r},\text{split},\text{tree}_{left},\text{tree}_{right}>) = exset\text{-}rep(\text{tree}_{left}) \cup {(\textbf{d,r})} \cup exset\text{-}rep(\text{tree}_{right}) $$
$Is\text{-}legal\text{-}kdtree$ : kd-tree 的所有节点,在其对应的 split 维,其左节点值始终小于等于该节点,右节点的值始终大于该节点。
搜索算法
最近邻搜索
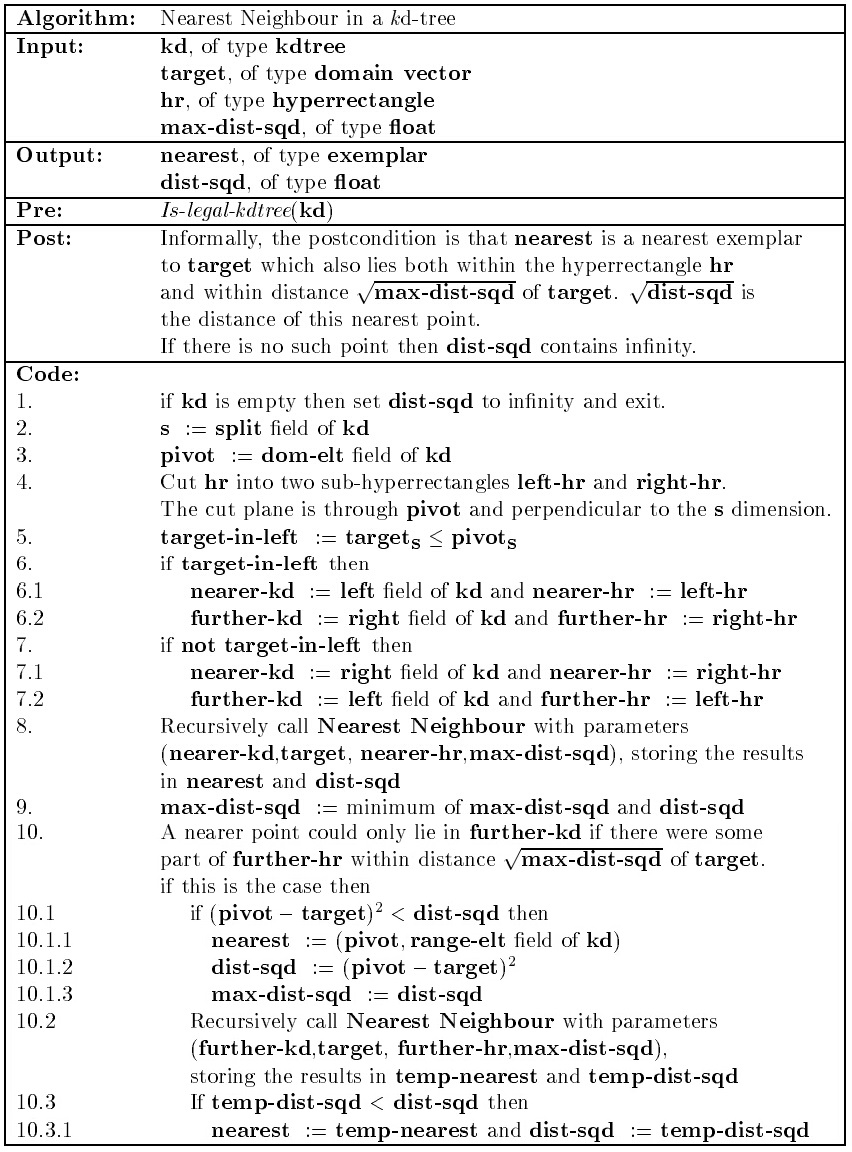
以上给出的为递归形式的、精确的最近邻算法流程。当 kd-tree 深度较大时,递归的调用需要消耗大量的系统资源,在实际应用过程中,往往采用非递归的形式,通过堆栈来进行回溯。
近似搜索
当能够接受最终搜索结果在误差 $\epsilon$ 内时,即可以通过近似的最近邻算法来实现,以一定的精度损失来换取搜索的速度。其思想与上述精确的最近邻算法一样,不同的是 Step 10。
- 精确搜索:是否需要在 further-kd 中搜索,根据半径为 $\sqrt{\textbf{max-dist-sqd}}$ 的超球体与 further-hr 是否相交而决定
- 近似搜索:是否需要在 further-kd 中搜索,根据半径为 $\frac{1}{1+\epsilon} \cdot \sqrt{\textbf{max-dist-sqd}}$ 的超球体与 further-hr 是否相交而决定
可以看出近似搜索的超球体半径更小,所以需要遍历的节点也更少,搜索更迅速。不过近似搜索不能保证找到真实的最近点,但其结果与真实的最近点在一定的相对误差范围之内。
优先搜索
优先搜索 [AM93a] 其思想为:对 further-kd 的搜索顺序是根据查询点到 further-hr 的距离来决定的。距离越近,则优先级越高。由于超球体的半径根据遍历找到的当前最近点的距离的减小而不断缩小,因此一定程度减少遍历的节点数。其实现过程描述如下:
- 当碰到一个非子叶节点时,先计算查询点到该节点划分的两个子 cell 的距离,将距离较远的 cell 对应的孩子节点加入到优先队列中。对距离较近的 cell 的孩子节点进行递归的访问
- 当到达子叶节点时,计算查询点到子叶节点中样本点的距离
- 根据距离的优先级,对队列中的节点进行递归访问
- 直到队列中的元素个数为0 或者 队列中节点对应的距离大于当前找到的最近点的距离的 $1/(1+\epsilon)$ 倍 (精确搜索时$\epsilon = 0$)
性能分析
维度的影响
搜索的时间复杂度至少为$O(\log_{2}{N})$(对于平衡二叉树),因为至少要到达一个子叶,其还与查询过程中所形成的超球体与 cell 的相交个数有关。(超球体的半径在搜索过程中随着当前所找到的疑似最近点的距离的减小而不断的缩小);最差为遍历整个样本集,时间复杂度为$O(n)$。当维度较高时,相交的 cell 将成指数增长,故 kd-tree 应用于高度维度数据集时,性能将急剧下降。
划分准则的影响
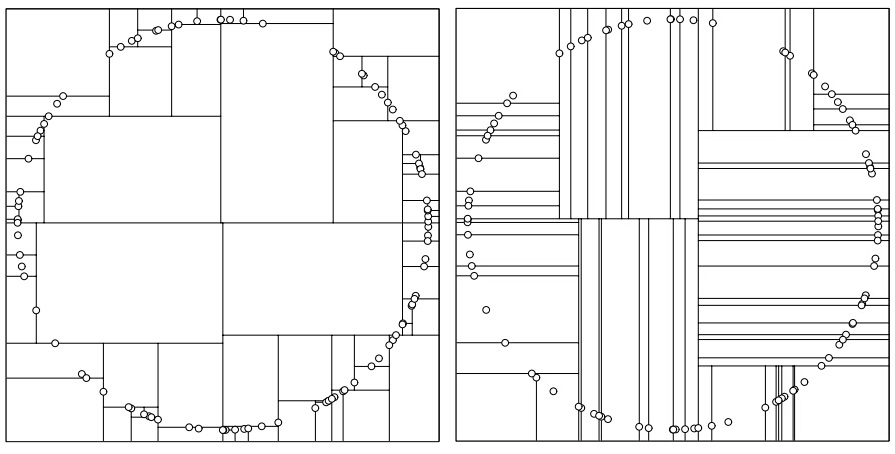
左图为 sliding midpoint rule 划分的结果(稍有不同的是:划分点选择的是数据集中最靠近中心的样本点 [$O(n)$],而非 cell 在该维度上的中心 [$O(1)$])。虽然树的分布出现部分不平横,但只有一个样本点的 cell 占据很大的区域,使得与超球体相交的 cell 数量很少,其较好的折中 kd-tree 的平衡性与 cell 的形状。
右图为 standard kd-tree splitting rule 划分的结果,得到的 kd-tree 为平衡二叉树,但都为非常细小的 cell,与超球体(二维空间上为圆形)相交的 cell 数目非常多,导致搜索过程中要遍历多个 further-kd,使得性能下降。当用具有最大方差的维度上中值 [Omohundro, 1987] 来划分时,情况将会略有改善。因为在最大方差的维度进行划分后,两个子 cell 在该维度上的方差将变得很小,使得下一次划分的维度几乎不会与上一次相同,而 standard kd-tree splitting rule 中选择最大 spread 划分会经常出现两次划分在同一维度上。但计算最大方差的时间复杂度要高于计算最大 spread 的时间复杂度。
参考资料以及推荐阅读:
- An intoductory tutorial on kdtrees
- ANN (Approximate Nearest Neighbor) Programming Manual
- http://web.stanford.edu/class/cs106l/handouts/assignment-3-kdtree.pdf 清晰易懂的介绍,内有关于 kd-tree c++ 编程实践的指导,推荐阅读。
blog comments powered by Disqus