Crazy Coder

Details Of Pagerank PageRank

30 January 2015

PageRank 技术详解

本文主要记录 PageRank 细节与原理，较为透彻的解释了 PageRank。不关心细节的同学可以看这篇文章：浅析PageRank算法，该文还简要的介绍了搜索引擎的基本原理以及 Topic-Sensitive PageRank。

主要思想

PageRank 通过网络浩瀚的超链接关系来确定一个页面的等级。Google把从A页面到B页面的链接解释为A页面给B页面投票，Google根据投票来源（甚至来源的来源，即链接到A页面的页面）和投票目标的等级来决定新的等级。

  • 链入 (In-coming links) 看作对页面的投票
    • 页面获得的投票越多，页面得分越高
  • 链出 (Out-going links) 的权重为该页面分数除以该页面链出个数。
    • 来自于重要页面的链入其投票所占权重越高 => 递归问题

下图以 y,a,m 3个页面为例:

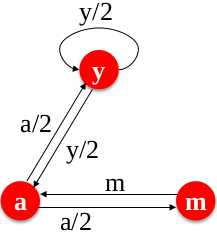
Drawing

定义每个页面的得分或排名 (rank) 为 $r_j$:

$$ r_j = \sum_{i\rightarrow j} r_i $$

则有

$$ \begin{matrix} r_y=1/2\cdot r_y + 1/2\cdot r_a + 0\cdot r_m \\ r_a=1/2\cdot r_y + 0~\cdot ~r_a + 1\cdot r_m \\ r_m=0~\cdot~ r_y + 1/2\cdot r_a + 0\cdot r_m \end{matrix} $$

三个方程，三个未知数且没有常数，此方程有无数个解。因此再加入一个约束 $r_y + r_a + r_m=1$, 则上述方程组的解为 $r_y=2/5$, $r_a=2/5$, $r_m=1/5$。当对于大规模页面所形成的图 (graph) 使用矩阵的形式表达更容易。例如，将上述方程组转化为矩阵形式为： $$ r = M \cdot r ~~~~~~ s.t. ~\sum_{i} r_i=1$$ 其中： $$ r = [r_y, r_a, r_m]^T $$ $$ M = \begin{bmatrix} 1/2 & 1/2 & 0\\ 1/2 & 0 & 1\\ 0 & 1/2 & 0 \end{bmatrix} $$

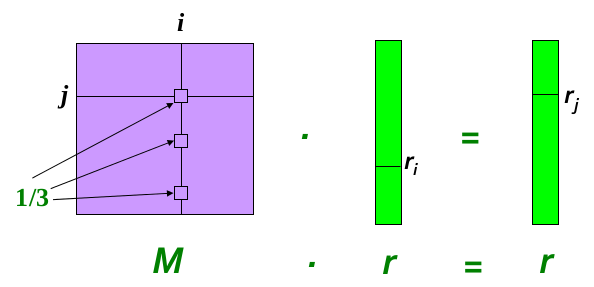
假设第$i$个页面，有3个链入，则其示意图如下： Drawing

Power Iteration Method

给定一个$N$节点的网络图（有向图），其中节点代表页面，边代表链接， Power Iteration 是一种简单的迭代算法：

  • 初始化: $ r^{(0)}=[1/N,\cdots,1/N]^T $
  • 迭代： $ r^{(t+1)}=M\cdot r^{(t)}$
  • 停止： $ |r^{(t+1)}-r^{(t)}|< \varepsilon$

Random Walk Interpretation

对于上述跌代算法的解释：可以假想有个随机的网站浏览者 (web surfer)

  • 在$t$时刻，浏览者在第$i$个页面上
  • 在$t+1$时刻，浏览者随机均匀地从页面$i$上选择一个链出到达了页面$j$
  • 以上过程一直独立地重复
  • $t$时刻，浏览者在第$i$个页面的概率为$p_{i}(t)$
  • 则$p(t)=[p_{1}(t),\cdots,p_{N}(t)]^T$为在这些页面上的概率分布

那么对于$t+1$时刻，浏览者可能在各个页面的概率为： $$p(t+1)=M\cdot p(t)$$ 最终的状态为 $$p(t+1)=M\cdot p(t)=p(t)$$ 则$p(t)$是这个 random walk 的稳态分布(stationary distribution)。（random walk 是一个 Markov processes）

是否始终会收敛

Situation 1: Spider trap

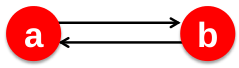
Drawing

例如： $$ \begin{matrix} Iter No. & 0 & 1 & 2 & 3 \\ --- & - & - & - & - \\ r_a & 1 & 0 & 1 & 0\\ r_b & 0 & 1 & 0 & 1 \end{matrix} $$

对于一组页面，其所有的链出都指向该组内部，将会导致 Spider trap。该组页面其会吸收所有外部的重要性，而不对外释放其自身的重要性（因为没有指向该组网页以外的链出），最终导致改组以外的页面得分皆为0。

Solution 1:

以下m节点，链出指向该组页面（即m）内部，将导致 Spider trap。

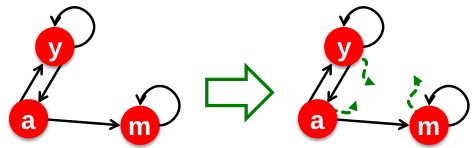
Drawing

$$ \begin{matrix} Iter No. & 0 & 1 & \cdots & \cdots \\ --- & - & - & - & - \\ r_y & 1/3 & 2/6 & \cdots & 0\\ r_b & 1/3 & 1/6 & \cdots & 0 \\ r_m & 1/3 & 3/6 & \cdots & 1 \end{matrix} $$

Google 对于 spider traps 的解决方案是：在每次选择链出时，浏览者有两种选择：

  • 有 $\beta$ 的概率，在当前节点的链出中随机均匀的选择一个
  • 有 $1-\beta$ 的概率，随机均匀的跳转到其他页面
  • $\beta$ 往往取 0.8 到 0.9

如此一来，经过若干次的选择，即可跳出 spider trap。如上图右侧所示。

Situation 2: Dead end

Drawing

例如： $$ \begin{matrix} Iter No. & 0 & 1 & 2 & 3 \\ --- & - & - & - & - \\ r_a & 1 & 0 & 0 & 0\\ r_b & 0 & 1 & 0 & 0 \end{matrix} $$

当某个网页只有链入，没有链出时，该节点即为 Dead end。这样的页面只吸收重要性，不释放重要性，将导致重要性泄漏。最终导致所有能够到达该节点的页面的得分为0。

Solution 2:

以下m节点，只有链入，没有链出，为一个 dead end。

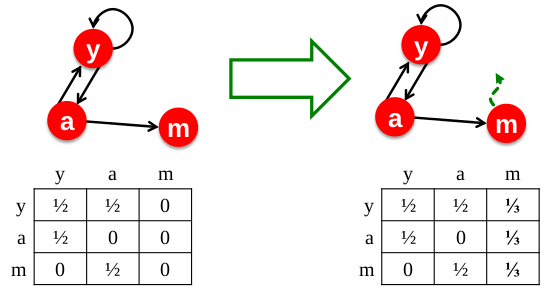
Drawing

$$ \begin{matrix} Iter No. & 0 & 1 & \cdots & \cdots \\ --- & - & - & - & - \\ r_y & 1/3 & 2/6 & \cdots & 0\\ r_b & 1/3 & 1/6 & \cdots & 0 \\ r_m & 1/3 & 1/6 & \cdots & 0 \end{matrix} $$

对此的解决方案为：

  • 下一刻，有概率1的可能，会随机均匀的跳转到任何页面。

如此一来，该点所吸收的重要性，将随机均匀的传递给任何一个页面，如上图右侧所示，注意其邻接矩阵中第三列的变化。

结论：

定理：对于任意的初始向量，将 power iteration 应用于一个马尔可夫转移矩阵P，当P为随机(stochastic)，非周期行(aperiodic),不可约的(irreducible)，必然会收敛于唯一的一个正的稳态向量。

  • A matrix is irreducible if it is not similar via a permutation to a block upper triangular matrix (that has more than one block of positive size).
  • Replacing non-zero entries in the matrix by one, and viewing the matrix as the adjacency matrix of a directed graph, the matrix is irreducible if and only if such directed graph is strongly connected.

上述的两种解决方案，使得矩阵$M$满足了该定理要求的三个性质，power iteration 将始终收敛于唯一解。

最终算法

加入上述两种解决方案后，页面$j$的得分为 (PageRank equation [Brin-Page, 98]):

$$ r_j=\sum_{i \rightarrow j} \beta \frac{r_i}{d_i}+(1-\beta)\frac{1}{n} $$

其中$d_i$为页面$i$的链出个数。此处假没有 dead ends，对此有两种处理方式：

  1. 可以对矩阵 $M$ 预处理，若页面$i$为 dead end，则$d_i=n$ （如上问 solution 2 中的方式，不建议使用这种方式，其使得 $M$ 变得稠密）。
  2. 直接让 dead ends 以概率1的可能进行随机跳转 (random teleport)（具体处理方式，见最终的算法）

将上式写成矩阵形式 (The Google Matrix $A$)： $$ A=\beta M+\frac{(1-\beta)}{n}\textbf{e}\cdot \textbf{e}^T $$

向量$\textbf{e}$中的值全为1。此时$A$满足上述定理中要求的三个性质。最终的 power iteration 迭代方程为： $$ r^{t+1}=A\cdot r^{t} $$

但在实际过程中，页面的数量是巨大的，假若网页数为$N$，对于每个页面得分以及矩阵 $A$ 元素用 4bytes 存储，则需要 $4\cdot (2N+N^{2})$ bytes。当对于10亿个页面，即 $N = 10^{9}$，对于矩阵 $A$ 即需要 $4\cdot 10^{18}$ bytes 来存储，对于如此庞大的矩阵，同时加载到内存中是几乎是不能的。通过观察可以发现，矩阵 $M$ 是个稀疏矩阵，由于加上了随机跳转的部分，而使得 $A$ 成为了稠密矩阵。将 $A=\beta M+\frac{(1-\beta)}{n}\textbf{e}\cdot \textbf{e}^T$ 展开，再利用 $\sum_{i=1}^{N} r_i=1$ 的性质，即可得到:

$$ r^{t+1}=\beta M \cdot r^{t} + \begin{bmatrix}\frac{1-\beta}{N}\end{bmatrix}_N $$

若每个页面平均有10个链接，则存储稀疏的 $M$ 矩阵只有大约只需要 $10N$ 的数量级存储单元。

完整的算法：

输入： 页面组成的图 Graph G (可能存在 spider traps 和 dead ends) 以及 $\beta$

输出： 得分向量 $r$

  • Initiation: $r_{j}^{(0)}=1/N$, $t=1$

  • do:

    • foreach page $j$
      if in-degree of page $j$ == 0 $~~~~r_{j}^{'(t)}=0$

      else $~~~~r_{j}^{'(t)}=\sum_{i \rightarrow j} \beta \frac{r_{j}^{(t-1)}}{d_i}$

    • Now re-insert the leaked PageRank:

      $\forall j: r_{j}^{(t)}=r_{j}^{'(t)} + \frac{1-S}{N}$, where $S=\sum_{j}r_{j}^{'(t)}$

    • $t=t+1$

  • while $\sum_{j}|r_{j}^{(t)}-r_{j}^{(t-1)}|>\varepsilon$

主要参考资料:
1. J. Leskovec, A. Rajaraman, J. Ullman (Stanford University) Mining of Massive Datasets

blog comments powered by Disqus