Optimization Algorithm optimization algorithm

优化方法

很多算法（机器学习，三维重建等）最终将归结于最优化问题，很多最优化问题则将归结于如何跳出局部最优，找到全局最优问题（好的初始值或加入随机因素等）。本文对常用的最优化方法做了个简要的归纳总结。

预备知识

Jacobian matrix

Jacobian matrix 是一阶偏导数以一定方式排列成的矩阵（而不是函数的一阶偏导数）。对于以下向量函数： $$ \mathbf{y}=F(\mathbf{x}); \quad s.t.: \mathbf{x} \in \mathbb{R}^n, \quad \mathbf{y} \in \mathbb{R}^m, \quad F:\mathbb{R}^n \mapsto \mathbb{R}^m $$

可以理解为：函数 $F(\mathbf{x})$ 由m个实函数 $F_{i}(\mathbf{x})$ 组成：

$$ \begin{bmatrix} y_{1}\\ \vdots \\ y_{m} \end{bmatrix} = \begin{bmatrix} F_{1}(x_{1},\cdots ,x_{n})\\ \vdots \\ F_{m}(x_{1},\cdots ,x_{n}) \end{bmatrix} $$

则 Jacobian matrix :

$$ J=J(F)(\mathbf{x})= \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \cdots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{bmatrix}_{m\times n} = \begin{bmatrix} \frac{\partial F_{1}}{\partial x_{1}} & \cdots & \frac{\partial F_{1}}{\partial x_{n}} \\ \vdots & \cdots & \vdots \\ \frac{\partial F_{m}}{\partial x_{1}} & \cdots & \frac{\partial F_{m}}{\partial x_{n}} \end{bmatrix}_{m\times n} $$

当 $\mathbf{y} \in \mathbb{R}^{1}$，即 $y=f(\mathbf{x})$, 则 $J=\begin{bmatrix} \frac{\partial y}{\partial x_{1}} & \cdots & \frac{y}{\partial x_{n}} \end{bmatrix}_{1 \times n} $

Hessian matrix

Hessian matrix 是实函数的二阶偏导数组成的方阵（而不是函数的二阶偏导数）：

$$ y=f(\mathbf{x}); \quad s.t.: \mathbf{x} \in \mathbb{R} ^{n}, \quad y \in \mathbb{R}, \quad F: \mathbb{R} ^n \mapsto \mathbb{R} $$

则 Hessian 矩阵为：

$$ H = \begin{bmatrix} \frac{\partial y}{\partial x_{1} \partial x_{1}} & \cdots & \frac{\partial y}{\partial x_{1} \partial x_{n}} \\ \vdots & \cdots & \vdots \\ \frac{\partial y}{\partial x_{n} \partial x_{1}} & \cdots & \frac{\partial y}{\partial x_{n} \partial x_{n}} \end{bmatrix}_{n\times n} $$

函数 $y=f(\mathbf{x})$ 一阶偏导数为：

$$ f'(\mathbf{x})=\frac{\partial y}{\partial \mathbf{x}}= \begin{bmatrix} \frac{\partial y}{\partial x_{1}} \\ \vdots \\ \frac{\partial y}{\partial x_{n}} \end{bmatrix}_{n\times 1} $$

由此可见，函数 $f'(\mathbf{x})$ 为向量函数 $\mathbb{R}^{n} \mapsto \mathbb{R}^{n}$, 输入为 $\mathbb{R}^{n}$ 空间中的向量，输出同样是 $\mathbb{R}^{n}$ 空间中的向量。 $f'(\mathbf{x})$ 的 Jacobian 矩阵即为 $f(\mathbf{x})$ 的 Hessian 矩阵。

优化方法

问题描述： 对于样本集 $\{(y^{1},\mathbf{x}^1), \cdots, (y^{m},\mathbf{x}^m)\}$, 求解参数 $\mathbf{\Theta} = \begin{bmatrix} \theta _{1},\cdots, \theta _{k} \end{bmatrix} ^{T} $ 使得样本集满足 $y^{i}=f(\mathbf{\Theta},\mathbf{x}^{i})$.

目标函数： $S(\mathbf{\Theta})=1/2 \cdot \sum_{i=1}^{m}r_{i}(\mathbf{\Theta})^{2}$，其中误差函数 $r_{i}(\mathbf{\Theta}) = f(\mathbf{\Theta},\mathbf{x}^{i}) - y^{i}$，$\mathbf{\Theta}$ 为函数自变量， $\mathbf{x}^{i}$ 视为常数。最小化该均方误差函数。

Gradient descent

梯度下降法：沿着梯度负方向更新参数。更新规则为：

$$ \mathbf{\Theta}^{t+1}=\mathbf{\Theta}^{t}-\gamma\cdot \nabla S(\mathbf{\Theta} ^{t}) $$

带入得：

$$ \mathbf{\Theta}^{t+1}=\mathbf{\Theta}^{t}-\gamma\cdot J_{r}^{T} \cdot \mathbf{r}(\mathbf{\Theta} ^{t}) \quad s.t. \quad (J_r)_{ij}=\frac{\partial r_{i}(\mathbf{\Theta}^t)}{\partial \theta_j} $$

即

$$ \begin{bmatrix} \theta_{1}^{t+1} \\ \vdots \\ \theta_{k}^{t+1} \end{bmatrix} = \begin{bmatrix} \theta_{1}^{t} \\ \vdots \\ \theta_{k}^{t} \end{bmatrix} - \gamma \cdot \begin{bmatrix} \frac{\partial f(\mathbf{\Theta}^{t},\mathbf{x}^1)}{\partial \theta_{1}} & \cdots & \frac{\partial f(\mathbf{\Theta}^{t},\mathbf{x}^1)}{\partial \theta_{k}} \\ \vdots & \cdots & \vdots \\ \frac{\partial f(\mathbf{\Theta}^{t},\mathbf{x}^m)}{\partial \theta_{1}} & \cdots & \frac{\partial f(\mathbf{\Theta}^{t},\mathbf{x}^m)}{\partial \theta_{k}} \end{bmatrix}^{T} \cdot \begin{bmatrix} f(\mathbf{\Theta}^{t},\mathbf{x}^1)-y^1 \\ \vdots \\ f(\mathbf{\Theta}^{t},\mathbf{x}^m)-y^m \end{bmatrix} $$

Newton method

牛顿法主要应用于找寻函数的零点，即方程 $f(x)=0$ 的根。

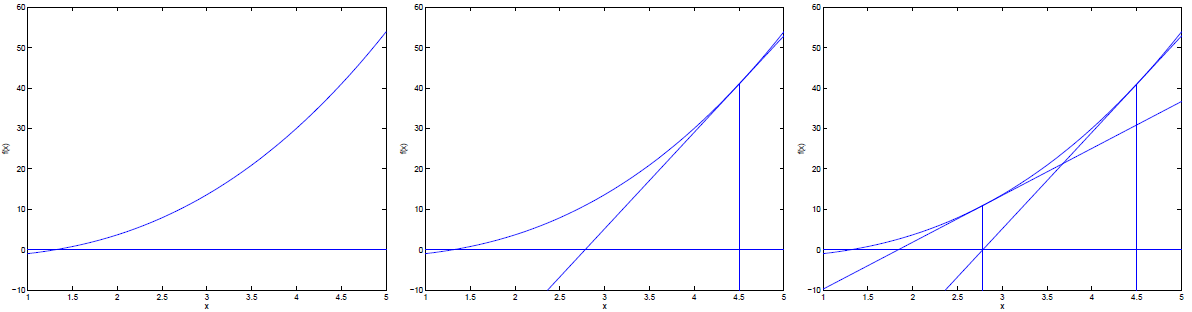
将此性质应用于目标函数的一阶偏导数 $f'(\mathbf{x})$，则 $f'(\mathbf{x})=0$ 的根即为函数 $f(\mathbf{x})$ 的极点。

找零点（根），$S(\mathbf{\Theta})=1/2 \cdot \sum_{i=1}^{m}r_{i}(\mathbf{\Theta})^{2}$ 的最小值，即为 $\mathbf{r}(\mathbf{\Theta})$ 的零点

更新规则：

$$ \mathbf{\Theta}^{t+1}=\mathbf{\Theta}^{t}-\gamma\cdot J_{r}^{-1} \cdot \mathbf{r}(\mathbf{\Theta} ^{t}) \quad s.t. \quad (J_r)_{ij}=\frac{\partial r_{i}(\mathbf{\Theta}^t)}{\partial \theta_j} $$

找极值，直接找 $S(\mathbf{\Theta})$ 导数为零的值

更新规则：

$$ \mathbf{\Theta}^{t+1}=\mathbf{\Theta}^{t}-\gamma\cdot H_{s}^{-1} \cdot \nabla S(\mathbf{\Theta}^{t}) \quad s.t. \quad (H_s)_{ij}=\frac{\partial ^{2} S(\mathbf{\Theta}^t)}{\partial \theta_i \partial \theta_j} $$

$$ \nabla S(\mathbf{\Theta} ^{t}) = \frac{\partial S(\mathbf{\Theta}^{t})}{\partial \mathbf{\Theta}}= \begin{bmatrix} \frac{\partial S(\mathbf{\Theta} ^{t})}{\partial \theta_1} \\\ \vdots \\ \frac{\partial S(\mathbf{\Theta} ^{t})}{\partial \theta_k} \end{bmatrix} $$

Gauss-Newton method

高斯牛顿法其基本思想为先用泰勒展开对 $f(\mathbf{\Theta},\mathbf{x})$ 进行线性近似，然后令 $\mathbf{r}(\mathbf{\Theta})=\mathbf{0}$ 推导而出。用于找 $\mathbf{r}(\mathbf{\Theta})$ 的零点。

更新规则： $$ (J_{r}^{T}\cdot J_{r})\cdot \mathbf{\Delta} = J_{r}^{T} \cdot \mathbf{r}(\mathbf{\Theta}^{t}) \quad s.t. \quad (J_r)_{ij}=\frac{\partial r_{i}(\mathbf{\Theta}^t)}{\partial \theta_j} $$

利用任意求解线性方程组方法求解上式 $\mathbf{\Delta} = \begin{bmatrix} \delta_{1},\cdots,\delta_{k} \end{bmatrix}^{T} $

$$ \mathbf{\Theta}^{t+1} = \mathbf{\Theta}^{t}-\mathbf{\Delta} = \mathbf{\Theta}^{t} - (J_{r}^{T}\cdot J_{r})^{-1}J_{r}^{T} \cdot \mathbf{r}(\mathbf{\Theta}^{t}) $$

当 $m=k$ 时，$(J_{r}^{T}\cdot J_{r})^{-1}J_{r}^{T} = J_{r}^{-1}$，其更新规则与 Newton method 找零点的更新规则相同

Levenberg Marquardt

L-M算法其基本思想为先用泰勒展开对 $f(\mathbf{\Theta},\mathbf{x})$ 进行线性近似，然后令 $\partial S(\mathbf{\Theta - \Delta})/ \partial \mathbf{\Delta}=\mathbf{0}$ 推导而出。其中加入了 damping factor: $\lambda$

更新规则： $$ (J_{r}^{T}\cdot J_{r}+\lambda \cdot diag(J_{r}^{T}\cdot J_{r}))\cdot \mathbf{\Delta} = J_{r}^{T} \cdot \mathbf{r}(\mathbf{\Theta}^{t}) \quad s.t. \quad (J_r)_{ij}=\frac{\partial r_{i}(\mathbf{\Theta}^t)}{\partial \theta_j} $$

利用任意求解线性方程组方法求解上式 $\mathbf{\Delta}$

$$ \mathbf{\Theta}^{t+1} = \mathbf{\Theta}^{t}-\mathbf{\Delta} = \mathbf{\Theta}^{t} - (J_{r}^{T}\cdot J_{r}+\lambda \cdot diag(J_{r}^{T}\cdot J_{r}))^{-1}J_{r}^{T} \cdot \mathbf{r}(\mathbf{\Theta}^{t}) $$

由上式可以看出，当 $\lambda = 0$ 时，上式等于 Gauss-Newton 法，当 $\lambda = \infty$ 时， $J_{r}^{T}\cdot J_{r}$ 相对于 $\lambda \cdot diag(J_{r}^{T}\cdot J_{r})$ 可以忽略不计，则上式等效于 Gradient descent， 各维上的更新步长与 $1/\lambda$ 以及该维对应于 $diag(J_{r}^{T}\cdot J_{r})$ 元素 $\sigma_{i}$ 的倒数 $1/\sigma_{i}$ 成正比。 $1/(\sigma_{i}\cdot \lambda)$ 即可看作梯度下降中的更新率 $\gamma$， $diag(J_{r}^{T}\cdot J_{r})$ 对角元素 $\sigma_{i}$ 越大，说明第 $i$ 维下降越快，对于 $\sigma_{i}$ 较小的维度，给予较大的步长，以便更快的收敛。

总结

• Newton method
  • 优点： 迭代次数少，精度较高，二次收敛
  • 缺点： 每次迭代需要求 Hessian 矩阵，代价高；且可能存在二阶偏导数求解困难的情况；当 Hessian 近似不可逆时，容易导致不收敛
• Gauss Newton method
  • 优点： 无需求解二阶偏导
  • 缺点： 仅适用于目标函数为平方和的最优化问题，需求解线性方程组，可能不收敛，线性收敛
• L-M algorithm
  • 优点： 比 Gauss Newton 更鲁棒（即离最终收敛的最小值较远，也可能收敛）
  • 缺点： 收敛速度往往比 Gauss Newton 慢